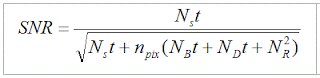Unsharp masking

Anche il filtro di "unsharp masking" o "maschera sfuocata" può essere classificato come un filtro differenziale come quelli già qui descritti in precedenza, il Median Coma Model e il Larson-Sekanina. Data infatti un'immagine $ f(x,y) $, è possibile sottrarre da essa un'altra immagine, ricavata dalla stessa, ma opportunamente sfuocata $ f_S (x,y) $ ed ottenere la così detta "maschera" $ g_M(x,y) $:
\begin{equation}
g_M(x,y) = f(x,y) - f_S (x,y)
\end{equation}
La sfuocatura può essere applicata sia con un filtro mediano, con un gaussiano o anche un laplaciano: le variazioni su grande scala sull'immagine originale non vengono intaccate da questi filtri, mentre i dettagli più fini sì, vengono per l'appunto "sfuocati". La "maschera" comporta il passo successivo per ottenere l'immagine finale $ g_F(x,y) $ opportunamente filtrata:
\begin{equation}
g_F(x,y) = f(x,y) - k \times g_M (x,y)
\end{equation}
Sempre nel caso del nostro programma di riferimento Astroart, il coefficiente $ k $ è per l'appunto il valore indicato con "coefficient" nella finestra dell' unsharp masking (vedi figura sotto), mentre il parametro "sigma" richiesto dalla stessa finestra determina l'entità della sfuocatura: maggiore è sigma e maggiore è la sfuocatura applicata alla maschera.

Come tutti i filtri anche l'unsharp masking tende a creare degli artefatti: quello particolarmente fastidioso per le immagini astronomiche viene spesso indicato con il termine dark ring o black ring, che consiste in un vistoso anello nero che avvolge le stelle più luminose dell'immagine filtrata.

Al centro gli artefatti "dark ring" conseguenti all'unsharp masking dell'immagine originale di sinistra. A destra lo stesso unsharp masking con attivata l'opzione "adattiva".

Gli artefatti ad anello sono dovuti alla sottrazione della maschera sfuocata che in certi punti può generare (anzi, certamente genera!) dei valori negativi. Per ovviare a questo è stata prevista un'ulteriore opzione: "adattiva" (o "adaptive") che tronca per l'appunto questi valori negativi riportandoli a zero.

Il filtro di Larson-Sekanina

E' senza dubbio il filtro più utilizzato per lo studio morfologico delle chiome cometarie. Descritto per la prima volta in un articolo dell'Astronomical Journal del 1984 degli astronomi Steven M. Larson del Lunar and Planetary Laboratory in Arizona e Zdenek Sekanina del Jet Propulsion Laboratory in California, consiste essenzialmente nel calcolare la differenza tra l'immagine originale e una sua nuova versione che è stata leggermente ruotata o spostata radialmente rispetto ad un punto centrale di riferimento (il falso nucleo della cometa). Questo filtro permette di rilevare variazioni luminose in piccola scala e in tutte le direzioni ripetto al nucleo dell'immagine originale. Una descrizione più dettagliata dell'algoritmo e utile per essere riprodotta con altri programmi di calcolo, la si può trovare qui in italiano, oppure qui in inglese.

I parametri che ne permettono l'utilizzo sono due: $ r $, in pixel e l'angolo $ \alpha $, in gradi.

Entrambi i parametri possono essere variati contemporaneamente ma possiamo capirne meglio il funzionamento se ne fissiamo uno a zero e variamo l'altro. Otteniamo così due casi:

• $ r $ = 0. 
  Variamo quindi solo l'angolo $ \alpha $. (normalmente  $ \alpha $ è compreso tra i 0° e i 15°)  Si aumenta il contrasto di tutti i particolari che hanno un gradiente angolare di luminosità rispetto all'origine del nostro sistema polare di coordinate (il falso nucleo); i particolari che si evidenziano sono in genere i jet o i vari dettagli dell'origine della coda cometaria. In figura é evidente il principale che da origine alla coda e che attraversa tutto il quadrante in alto a sinistra dell'immagine.
  Questo gradiente, calcolato in corrispondenza dei punti P-P1 e P-P2, esalta il contrasto della struttura principale che forma la coda in uscita dal nucleo della cometa, mentre dalla parte opposta a seconda della scala dell'immagine e dell'evento, può evidenziare delle deboli strutture a fontana provenienti da punti ad elevata attività sulla superficie del nucleo. L'angolo di rotazione $ \alpha $ deve essere scelto accuratamente ed accertarsi che tutte le strutture siano correttamente evidenziate: infatti, se l'angolo è troppo piccolo, la struttura nell'immagine originale può sovrapporsi a quella nell'immagine ruotata producendo così una struttura più sottile di quella che è nella realtà; di contro, se l'angolo è troppo grande è molto probabile imbattersi in artefatti e quindi in strutture non reali. 
  
  

  

  r = 0

  $ \alpha $ = 0.
  Per spostamenti rotazionali nulli, modificando il valore di $ r $ (generalmente da zero a qualche pixel), si aumenta il contrasto di tutti i particolari che hanno un gradiente radiale di luminosità rispetto al falso nucleo. Essendo nulli gli spostamenti rotazionali, tutti i jet che si protendono dal nucleo verso l'esterno non sono più visibili. Questo tipo di elaborazione permetterà invece di mettere in evidenza aloni, strutture a spirale e gusci di polvere e gas che compongono gli strati più interni della chioma. 
  
  

  

  α = 0

Il filtro di Larson-Sekanina è molto potente nell'evidenziare la presenza di eventuali strutture nascoste della chioma cometaria. Tuttavia occorre prestare grandissima attenzione nell'uso dei due parametri e ricordarsi che trattandosi di un filtro "differenziale" cioè basato sulla differenza di due immagini, esso può essere considerato come una "derivata" in tutte le direzioni della funzione che rappresenta l'immagine $ f(x,y) $ e come tale quindi, l'immagine filtrata rappresenta una mappa delle variazioni di luminosità all'interno della struttura cometaria e non delle strutture stesse.

Si tratta dunque di variare i parametri $ r $ e $ \alpha $: prestando attenzione a non generare eventuali artefatti; questo problema si può almeno in parte evitare variando i parametri entro un certo range stabilito e un determinato passo di variazione (es.$ 0.1 < r < 2.0 $ con passi di 0.1 pixel), salvare le immagini filtrate così ottenute e quindi mediarle tutte insieme.

Qui sotto un breve filmato sull'utilizzo del filtro con il programma Astroart 5.0:

Il rapporto segnale-rumore (SNR)

A causa della natura quantistica della luce, il rilevamento dei fotoni (con un dispositivo come il CCD) è sempre un processo casuale dominato dalla statistica di Poisson: la distribuzione poissoniana (dal matematico francese Simeon Poisson, 1781-1840).
La distribuzione di Poisson è più comunemente utilizzata per modellare il numero di eventi casuali di alcuni fenomeni in un'unità specificata di spazio o di tempo: è come una distribuzione gaussiana (a campana) con la larghezza determinata dalla radice quadrata del numero totale di conteggi . Quando si cerca di misurare un evento poissoniano come un fotone rilevato da una camera CCD, il rumore di conteggio associato è dato dalla radice quadrata del segnale, quindi il rumore N associato ad un segnale S è √ S ​​e il rapporto segnale rumore (o S / N o SNR) è:

Questa relazione fondamentale è la chiave per capire come il rumore influenza la nostra osservazione: in realtà questo rapporto mostra il limite naturale superiore del SNR. Non fa differenza se un oggetto è luminoso o debole o se prendiamo esposizioni lunghe o corte con telescopi grandi o piccoli: tutto dipende da quanti fotoni (S), siamo in grado di raccogliere: il SNR non potrà mai essere superiore a √ S .
In realtà ci sono altre fonti di rumore in una immagine CCD che mantengono il SNR del nostro oggetto di interesse inferiore al limite teorico di √ S.
 Ecco un elenco dei più importanti di essi:
• Rumore di lettura (readout noise): è il numero di elettroni per pixel introdotti nel segnale finale sulla lettura del dispositivo CCD. Valori tipici nei moderni CCD sono entro i 10 elettroni / pixel;
• Rumore termico (dark count): è il numero di elettroni termici generati al secondo per pixel ad una temperatura specifica. I valori tipici sono pochi elettroni o frazioni di elettroni al secondo nel caso CCD raffreddato;
• Rumore di fondo (background noise): non si tratta di un rumore strumentale, ma è di grande importanza. L'inquinamento luminoso del fondo cielo, sia artificiale che naturale, come la presenza della luna, contribuiscono al segnale di fondo raccolto dal CCD, ma questi non si traducono in un aumento del segnale dell'oggetto di nostro interesse.
• Rumore di processing: ogni volta che fate un po 'di elaborazione delle immagini di base, come la sottrazione del dark frame e la divisione per il flat field si combinano i numeri incerti con altri numeri incerti. Dal momento che, in generale, si tratta di fonti indipendenti di rumore, il rumore totale finale si sommerà quadraticamente. Ad esempio, se abbiamo rumore da tre sorgenti con valori N1, N2 e N3, il rumore totale sarà:

Facciamo un esempio con i numeri reali per vedere, quanto il rumore di fondo potrebbe influire sul rumore complessivo di un'immagine e degradare la qualità dell'immagine stessa.
Supponiamo, per semplicità, che il seeing sia talmente buono da far cadere la nostra fonte di segnale (una stella) completamente all'interno di un pixel. Il segnale complessivo accumulato dal pixel è di 900 conteggi: 400 di loro provengono dal fondo cielo mentre 500 provengono dalla luce della stella. La combinazione stella+cielo ha un rumore di √ 900 = 30 conteggi su quel pixel e questo darebbe un SNR di 900/30 = 30. Ma questo non è il modo corretto per valutare l'SNR. Il segnale della nostra fonte è infatti di 500 conteggi, dunque una stima migliore del SNR è 500/√900 = 16,7. In realtà, il vero SNR è ancora più basso: poiché non abbiamo alcun modo di sapere che il fondo cielo è esattamente di 400 conteggi (lo sfondo del cielo è a sua volta influenzata dal rumore poissoniano!) dobbiamo aggiungere il contributo del rumore dal cielo (√ 400 = 20) a quello della stella più il rumore del fondo cielo ancora (√400+500 =30 ), allora si ha:

Questo significa che siamo in grado di misurare la luminosità della stella con una precisione di ± 1/13.8 ovvero circa ± 7%.
Ma cosa succede se cerchiamo di prendere le immagini della stella stessa sotto un cielo luminoso urbano dove lo sfondo è, per esempio, 5000 conteggi invece di 400? Seguendo l'esempio precedente abbiamo ora:

Ora la stella è appena visibile: infatti un valore tipico del SNR per una stella rilevabile è ≥ 3, e siamo in grado di misurare la sua luminosità con una precisione di ± 20% soltanto. In pratica, tuttavia, altre fonti di rumore come rumore di lettura e rumore termico abbasserà ancora di più questo valore.
L'esempio precedente serve spiegare perché si puossono vedere stelle più deboli (e/o dettagli di nebulose) sotto un cielo più scuro: è semplicemente e sempre una questione di SNR.
Una delle equazioni più utilizzati per descrivere il SNR è quello di Merline & Howell (1995, Expt Astron, 6, 163):

Dove:

N_s = numero dei fotoni (segnale) per pixel raccolti dall'oggetto in esame;
N_B = numero dei fotoni per pixel provenienti dal fondo cielo;
N_D = numero di elettroni per pixel generati dalla corrente di buio;
N_R = numero di elettroni per pixel generati dal rumore di lettura (readout noise);
n_pix = numero dei pixels implicati nel calcolo di ogni termine di rumore;
n_B = numero dei pixel di fondo cielo utilizzati nella stima del livello medio di fondo cielo;
G = guadagno (gain) del CCD (electroni/ADU)
σf² = stima dell'errore 1-sigma introdotto dal convertitore A/D: il suo valore può essere approssimato a 0.289.


Vediamo un esempio pratico con qualche numero reale. Il CCD è un SITe502 con queste caratteristiche (dalla scheda tecnica del modello Apogee AP7p):

G = 4.4 elettroni / ADU
N_R = 10.2 elettroni
N_D = 1.4 elettroni / pixel / secondo (a temp. -27 Gradi.)

Supponiamo una esposizione di 60 secondi ad una temperatura di -27 gradi e, per semplicità, che la scala immagine CCD è di 3 arcsec / pixel e che il seeing sia tale da permettere al segnale proveniente dalla stella di ricadere completamente nel raggio di 1 pixel: dopo la sottrazione del valore del fondo cielo, nel nostro pixel troviamo N_s = 12015 ADU ∙ G = 12015 ∙ 4,4 = 52866 elettroni. Supponiamo anche di misurare il il fondo cielo all'interno di una box di 20x20 pixel vicino alla stella e che si trovi un valore medio di 3215 ADU / pixel (quindi N_B = 3215 ∙ G = 14146 elettroni).
Sostituendo questi valori nella Eq. 2 si ottiene (si noti che tutti i valori utilizzati sono espressi in elettroni, non in ADU):

Con questi numeri si può facilmente notare che se si ignora il secondo termine al divisore, il SNR assume il valore ideale di un puro rumore di Poisson:

e che, se prendiamo in considerazione le condizioni del fondo cielo, la corrente di buio e il rumore di lettura solo abbiamo ancora:

Si noti che è possibile utilizzare la seguente formula semplificata senza fare un grande errore:

Oppure, se siamo interessati a una previsione del valore SNR che può essere ottenuto per un dato sistema CCD e un tempo di integrazione t, l' Eq. 3 può essere scritta come:

dove N_s, N_B e N_D, ora sono da intendersi come conteggi in elettroni (fotoni) al secondo se t è espresso in secondi. Questa equazione illustra una regola empirica preziosa relativa SNR di un'osservazione: il SNR è proporzionale a √ t e non di t stesso.

Il filtro M.C.M.: un altro esempio

Per illustrare meglio la funzionalità e l'efficacia del filtro M.C.M., analizziamo un'immagine ripresa da Nick Howes al Faulkes Telescope North (un telescopio completamente remotizzato di 2 m. di diametro posto alle Hawaii presso l'Haleakala Observatory e gestito dall'organizzazione LCOGT). La cometa oggetto della ripresa stavolta è la C/2007 Q3 (SIDING SPRING).


Anche in questo caso come è possibile notare dalla traccia delle stelle fisse, si tratta in realtà di un'immagine composta dalla somma di 11 frames ripresi con un normale filtro rosso (di Bessel) a banda larga. Ma la cosa notevole di questa immagine è il campionamento: 0.2785 arcosecondi/pixel con un seeing medio di 1.3 secondi d'arco! (In realtà abbastanza normale per il cielo delle Hawaii). Fantastico! Sembra che i "prof" del FTN abbiano preso alla lettera le mie considerazioni sul principio di Nyquist. Si tratta dunque di una serie di immagini riprese in condizioni che noi poveri astrofili italiani ben difficilmente possiamo ritrovare (compreso il telescopio da 2 metri...).
Ebbene se applichiamo il filtro M.C.M. alla chioma di questa cometa, ecco cosa scopriamo:


Nella breve sequenza qui sopra possiamo notare in bianco e nero l'immagine originale e in falsi colori la relativa trasformazione dopo l'applicazione del filtro. Appare evidentissimo nella parte in basso a destra la presenza del frammento distaccatosi dal nucleo della cometa, accompagnato da un'area di forte attività.

Nel filmato che segue viene riportata una sequenza più lunga formato dalle immagini riprese il 17-20-27 marzo e 2-12 aprile: è possibile notare la progressiva attenuazione dell'evento.

Mentre, per chi capisce l'inglese decisamente stretto di Nick Howes, ecco una sua intervista a riguardo su YouTube:




Infine vi riporto alcune considerazioni di Giannantonio Milani, responsabile della Sezione di Ricerca Comete UAI e coordinatore del gruppo CARA, riguardo all'utilizzo e al funzionamento del filtro M.C.M.:

In linea teorica un nucleo sferico che emette polveri in tutte le direzioni a velocità e quantità costante dovrebbe creare una chioma perfettamente simmetrica e , in questi caso, se applicassimo il filtro MCM otterremmo una chioma "regolare" sostanzialmente identica all'originale.
Ma l'effetto di accelerazione dovuto alla pressione di radiazione solare sui grani di polvere e il fatto che i nuclei cometari non emettano gas e polveri in modo isotropo, rende spesso le chiome cometarie tutt'altro che simmetriche. A questo possiamo anche aggiungere gli effetti dovuti alla prospettiva e al modo in cui la nostra linea di vista e' posizionata rispetto al Sole a e ai dettagli della chioma.
L'MCM, creandoci una chioma "regolare", che rappresenta l'andamento medio della chioma reale, ci permatte di mettere in evidenza anche piccolissime disomogeneità nella chioma.
Spesso potremo avere un eccesso di luminosita' in direzione del Sole, in corrispondenza del lato diurno del nucleo maggiormente eccitato dalla radiazione solare.
Ma a volte, ad esempio in presenza di fenomeni di disgregazione del nucleo, potremmo anche trovare un eccesso di luminosità in direzione della coda.
L'interpretazione non è mai semplice o scontata ed è resa più complessa dal fatto che generalmente le osservazioni sono effettuate con filtri a banda larga (BVRI o RGB) che non discriminano in modo rigoroso tra emissioni gassose e polveri.
Nel blu e verde nelle comete attive avremo spesso una forte contaminazione gassosa, nel rosso dominerà più la polvere ma possono essere presenti ancora emissioni sia nella chioma che nella coda.
Interpretazioni di immagini senza filtri sono ancora più problematiche perchè per nulla selettive.
Risultati più incisivi da un punto di vista scientifico richiederebbero l'utilizzo di filtri a banda stretta che però comportano diversi problemi aggiuntivi, anche di calibrazione, ed il fatto di dover avere una cometa luminosa per raggiungere un elevato rapporto segnale/rumore.
L' MCM non fornisce di norma un andamento 1/r ma ci si può aspettare che in generale non se ne discosti troppo, salvo in caso di eventi peculiari come frammentazioni del nucleo, outburst, ecc..
la formula più corretta potrebbe essere 1/r^n con n=1 se ovviamente fossimo uguali a 1/r.
In caso di evidenti disomogeneità però non rispetterà esattamente neppure questa formula, che sarà tuttavia indicativa.

Il filtro M.C.M. (normalizzazione radiale)

M.C.M. è l'acronimo di Median Coma Model che possiamo tradurre in "modello mediano della chioma". E' conosciuto anche con il nome di "normalizzazione radiale".
Lo scopo di questo filtro è quello di creare, partendo da un'immagine di una cometa $ f(r,\theta) $ (in un sistema di coordinate polari), un modello sintetico della chioma "regolare" $ g(r,\alpha) $, cioè ottenuto mappando, in senso radiale con dei cerchi concentrici di raggio $ r $, tutti i pixel dell'immagine che la compongono e mediandoli tra loro: così facendo si eliminano tutte le eventuali "disuniformità" morfologiche contenute nella chioma stessa.
\begin{equation} g(r,\alpha) =\frac{\sum_{\theta=0}^{360} f(r,\theta)}{C_{r}} \end{equation} dove $ C_{r} $ rappresenta il numero di pixel contenuti nel cerchio di raggio $ r $, centrato sul nucleo della cometa. Questa chioma "regolare" verrà successivamente sottratta dall'immagine originale mettendo in evidenza tutti quei particolari che normalmente sono immersi nella luminosità uniforme della chioma.

Come si installa
Si installa come tutti i plug-in di Astroart. Semplicemente scaricate il plug-in con l'immagine d'esempio qui e copiate il file picoma9.dll all'interno della cartella principale del programma (solitamente la cartella C:\Programmi\MSB\Astroart). Quando rilancerete il programma, nel menu Plug-in comparirà la nuova voce MedComet Coma Model.

Come si utilizza
Ovviamente la prima cosa da fare è caricare un'immagine di una cometa, possibilmente con un buon rapporto segnale-rumore. Potete utilizzare quella contenuta nel pacchetto del plug-in appena scaricato (Bq2@650.fit) della C/2004Q2 (Machholz) se non ne avete già una in archivio.


Questa immagine è stata ripresa all' Osservatorio di Cavezzo il 3 gennaio del 2005 con una camera CCD della Apogee, la Ap7p con 512x512 fotoelementi quadrati da 24 micron, al fuoco Newton 0.4m. f/5.5 e con filtro interferenziale centrato sui 650nm con banda passante di 10nm (per isolare la sola emissione delle polveri). Si tratta in realtà della somma di 30 immagini da 30 secondi per un totale d'integrazione di 900 secondi. Il Nord è in alto e l'Est a sinistra. Il campionamento dell'immagine è di 2,24 secondi d'arco per fotoelemento. Nonostante il potere risolutivo (teorico) dell'apertura del telescopio (limite di Dawes = 0,3") siamo parecchio sottocampionati (2,24"/pixel appunto contro i necessari 2,5/4=0,625"/pixel). Per di più il seeing medio in questa serie di immagini è di circa 2,5 secondi d'arco (confrontabile con il campionamento) quindi sarebbe stato comunque inutile campionare per risolvere il limite di Dawes (0,3/4 = 0,075 arcsec/pixel). La cometa era distante 0,349 U.A. dalla Terra, quindi sul piano dell'immagine corrisponde ad una scala di 568 km per pixel. Dato che che il nostro campionamento coincide circa con il seeing medio, non riusciamo nemmeno a risolvere quest'ultimo, dunque con ogni probabilità i più piccoli dettagli risolvibili in questa immagine saranno intorno ai 568x4 = 2272 km (ricordiamo che il "x 4" deriva dal teorema di Nyquist "modificato" ). Diciamo dunque che, molto conservativamente, avremo una risoluzione intorno ai 2000 km circa.
Fatte tutte queste premesse, comunque indispensabili per capire la scala dei fenomeni che andremo a vedere, lanciamo il plug-in del M.C.M.: ci troveremo una finestra di dialogo così:


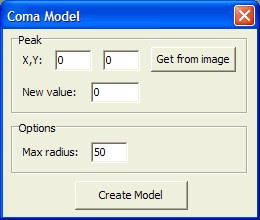
Per il momento non scriviamo niente. Posizioniamo il cursore intorno al centro della chioma e muoviamolo lentamente: non appena si trasforma in un piccolo cerchietto facciamo click con il mouse. Il cerchietto identifica la zona del baricentro fotometrico della chioma e il click ne fissa in memoria le coordinate. Ora facciamo click sul pulsante "Get from image" e vedremo che le caselle di testo X,Y verranno automaticamente compilate con le coordinate memorizzate. Lasciamo inalterato il valore "New value": questo ci permetterà di visualizzare con un piccolo puntino nero la probabile posizione del falso nucleo della cometa nell'immagine del modello della chioma. Eventualmente, se non vogliamo questo, possiamo inserire il valore (in ADU) che leggiamo in corrispondenza del pixel memorizzato. Il valore "Max Radius" è sarà il raggio massimo del modello della chioma che vogliamo creare. Con la grandezza del nostro sensore di 512x512 pixel e considerando il fatto che con ogni probabilità il campo coperto in questa immagine è completamente occupato dalla chioma della cometa, possiamo tranquillamente impostare un valore di 250 pixel. Possiamo renderci conto del piccolo campo inquadrato rispetto alla totalità della cometa, confrontando la nostra immagine con una delle tante a largo campo fatte nella stessa data nello splendido archivio della Sezione Comete UAI, ideato e poi gestito per tanto tempo dall'infaticabile Rolando Ligustri e ora manutenuto dal bravissimo Walter Borghini.

Questa immagine di Rolando Ligustri della cometa C/2004Q2 (Machholz), fatta sempre il 3 gennaio 2005, copre un campo di 3,6x2,2 gradi. Il riquadro in rosso corrisponde all'incirca al campo di 20'x20' coperto dalla nostra immagine in esame. In questa bellissima immagine di Rolando si possono notare le due code: quella lunga, sottile e leggermente disconnessa verso Est (a sinistra) è la coda di gas, mentre quella più ampia e regolare verso sud (in basso) è quella di polveri.

E' evidente che la chioma della cometa è ben più ampia di quella ripresa nella nostra immagine, tuttavia a noi interessa mettere in evidenza le eventuali strutture in piccola scala nell'intorno del falso nucleo. Applichiamo dunque il plug-in con i parametri già riportati sopra. Otteniamo una nuova immagine con la rappresentazione del modello di chioma.

Le stelle sono scomparse (e così deve essere in quanto il modello "mediano" della chioma deve eliminare tutte le disuniformità, anche quelle che non appartengono alla chioma). Abbiamo un modello di chioma regolare con un andamento classico 1/r, come possiamo facilmente constatare attraverso la funzione Profilo del programma Astroart:


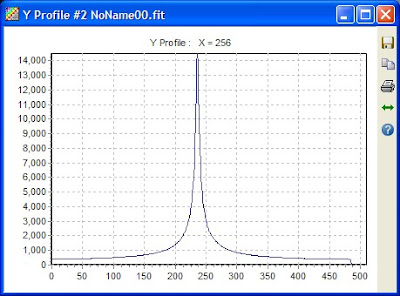
La particolarità di questo modello sintetico di chioma cometaria è che non è stato ricavato da una semplice legge matematica, come appunto può essere la funzione iperbole I = 1/r del modello classico, bensì è stata ricavata dai valori originali della nostra immagine opportunamente mediati lungo cerchi concentrici. La cosa non è banale, perchè noi non sappiamo a priori quale degli infiniti andamenti 1/r può assumere la chioma. Notiamo inoltre che, anche se in questo caso poco vistosamente, i due rami d'iperbole non sono simmetrici rispetto il centro della chioma: praticamente per ogni direzione del profilo che noi consideriamo otteniamo diversi valori dell'andamento 1/r.

Basta fare una semplice rappresentazione cartesiana di soli tre di questi andamenti per rendersene conto:

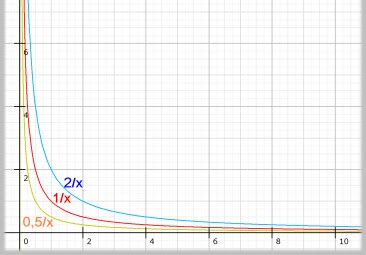
Abbiamo dunque ottenuto un modello di chioma che si adatta perfettamente a quello della chioma originale. Ora possiamo sottrarlo all'immagine originale. Si seleziona l'immagine originale (semplicemente cliccando sulla sua finestra) e si esegue il comando dal menu Aritmetica -> Sottrai. La nuova immagine, molto scura, va visualizzata con i livelli corretti: il modo più veloce è quello di attivare i livelli automatici con un semplice click sulla barra di stato grigia della finestra immagine (quella in basso dove compaiono i numeri delle soglie di visualizzazione), oppure si può procedere manualmente con i cursori posti sulla banda dei grigi nella parte destra del desktop di Astroart.


Come si interpreta
Qui viene il difficile. Cosa stiamo osservando? Qui veramente ci avviciniamo ad un argomento un po' pericoloso in quanto non è difficile fare delle speculazioni completamente errate. dobbiamo sempre ricordare che stiamo osservando un oggetto tridimensionale proiettato su un piano bidimensionale (l'immagine CCD appunto) al quale abbiamo sottratto un modello di chioma ricavato dall'immagine proiettata. Proviamo ad applicare una palette in falsi colori:



La palette in falsi colori (denominata "Arcobaleno" nelle palette di Astroart) associa i colori più caldi (bianco-giallo-rosso) alle intensità luminose più elevate e i colori più freddi (verde-blu-nero) alle luminosità via via inferiori e mostra chiaramente due cose:

1. Su larga scala, la parte destra dell'immagine (verso ovest) i pixel hanno una colorazione nero blu: se si scorre con il cursore si può chiaramente constatare che questo corrisponde a valori (in ADU) negativi, quindi la presenza di polveri della cometa in quella zona è decisamente inferiore a quella contenuta nel modello di chioma creato (prendendo come "zero" il valore corrispondente alla sottrazione "perfetta" del modello sull'immagine originale, in quella zona i valori si aggirano mediamente intorno ai -100 ADU). Al contrario, verso Est (colorazione verde azzurro) i valori sono ben oltre i +100 ADU e questo può suggerire una concentrazione di polveri maggiore rispetto a quella contenuta nel modello
2. Su piccola scala si nota un lobo molto luminoso verso Ovest, con intensità che a volte superano i 2000 ADU e due lobi in direzione Nord e Sud con intensità ancora una volta negative ( < -100 ADU). E' chiaro che nel primo caso si tratta di una zona con forte concentrazione di polveri, sempre rispetto al modello della chioma, mentre più misteriosa è la geometria dei due lobi poveri di polveri in direzione Nord-Sud.

Tuttavia una conformazione geometrica della chioma del tutto simile a questa (visibile qui), anche se per un'altra cometa e su una scala un po' più piccola, è stata ripresa dall'Hubble Space Telescope e successivamente elaborata (con un filtro immagino simile al mio M.C.M.) da Harold A. Weaver della Johns Hopkins University.