La distribuzione di Poisson è più comunemente utilizzata per modellare il numero di eventi casuali di alcuni fenomeni in un'unità specificata di spazio o di tempo: è come una distribuzione gaussiana (a campana) con la larghezza determinata dalla radice quadrata del numero totale di conteggi . Quando si cerca di misurare un evento poissoniano come un fotone rilevato da una camera CCD, il rumore di conteggio associato è dato dalla radice quadrata del segnale, quindi il rumore N associato ad un segnale S è √ S e il rapporto segnale rumore (o S / N o SNR) è:
Questa relazione fondamentale è la chiave per capire come il rumore influenza la nostra osservazione: in realtà questo rapporto mostra il limite naturale superiore del SNR. Non fa differenza se un oggetto è luminoso o debole o se prendiamo esposizioni lunghe o corte con telescopi grandi o piccoli: tutto dipende da quanti fotoni (S), siamo in grado di raccogliere: il SNR non potrà mai essere superiore a √ S .
In realtà ci sono altre fonti di rumore in una immagine CCD che mantengono il SNR del nostro oggetto di interesse inferiore al limite teorico di √ S.
Ecco un elenco dei più importanti di essi:
• Rumore di lettura (readout noise): è il numero di elettroni per pixel introdotti nel segnale finale sulla lettura del dispositivo CCD. Valori tipici nei moderni CCD sono entro i 10 elettroni / pixel;
• Rumore termico (dark count): è il numero di elettroni termici generati al secondo per pixel ad una temperatura specifica. I valori tipici sono pochi elettroni o frazioni di elettroni al secondo nel caso CCD raffreddato;
• Rumore di fondo (background noise): non si tratta di un rumore strumentale, ma è di grande importanza. L'inquinamento luminoso del fondo cielo, sia artificiale che naturale, come la presenza della luna, contribuiscono al segnale di fondo raccolto dal CCD, ma questi non si traducono in un aumento del segnale dell'oggetto di nostro interesse.
• Rumore di processing: ogni volta che fate un po 'di elaborazione delle immagini di base, come la sottrazione del dark frame e la divisione per il flat field si combinano i numeri incerti con altri numeri incerti. Dal momento che, in generale, si tratta di fonti indipendenti di rumore, il rumore totale finale si sommerà quadraticamente. Ad esempio, se abbiamo rumore da tre sorgenti con valori N1, N2 e N3, il rumore totale sarà:
Facciamo un esempio con i numeri reali per vedere, quanto il rumore di fondo potrebbe influire sul rumore complessivo di un'immagine e degradare la qualità dell'immagine stessa.
Supponiamo, per semplicità, che il seeing sia talmente buono da far cadere la nostra fonte di segnale (una stella) completamente all'interno di un pixel. Il segnale complessivo accumulato dal pixel è di 900 conteggi: 400 di loro provengono dal fondo cielo mentre 500 provengono dalla luce della stella. La combinazione stella+cielo ha un rumore di √ 900 = 30 conteggi su quel pixel e questo darebbe un SNR di 900/30 = 30. Ma questo non è il modo corretto per valutare l'SNR. Il segnale della nostra fonte è infatti di 500 conteggi, dunque una stima migliore del SNR è 500/√900 = 16,7. In realtà, il vero SNR è ancora più basso: poiché non abbiamo alcun modo di sapere che il fondo cielo è esattamente di 400 conteggi (lo sfondo del cielo è a sua volta influenzata dal rumore poissoniano!) dobbiamo aggiungere il contributo del rumore dal cielo (√ 400 = 20) a quello della stella più il rumore del fondo cielo ancora (√400+500 =30 ), allora si ha:
Questo significa che siamo in grado di misurare la luminosità della stella con una precisione di ± 1/13.8 ovvero circa ± 7%.
Ma cosa succede se cerchiamo di prendere le immagini della stella stessa sotto un cielo luminoso urbano dove lo sfondo è, per esempio, 5000 conteggi invece di 400? Seguendo l'esempio precedente abbiamo ora:
Ora la stella è appena visibile: infatti un valore tipico del SNR per una stella rilevabile è ≥ 3, e siamo in grado di misurare la sua luminosità con una precisione di ± 20% soltanto. In pratica, tuttavia, altre fonti di rumore come rumore di lettura e rumore termico abbasserà ancora di più questo valore.
L'esempio precedente serve spiegare perché si puossono vedere stelle più deboli (e/o dettagli di nebulose) sotto un cielo più scuro: è semplicemente e sempre una questione di SNR.
Una delle equazioni più utilizzati per descrivere il SNR è quello di Merline & Howell (1995, Expt Astron, 6, 163):
Dove:
Ns = numero dei fotoni (segnale) per pixel raccolti dall'oggetto in esame;
NB = numero dei fotoni per pixel provenienti dal fondo cielo;
ND = numero di elettroni per pixel generati dalla corrente di buio;
NR = numero di elettroni per pixel generati dal rumore di lettura (readout noise);
npix = numero dei pixels implicati nel calcolo di ogni termine di rumore;
nB = numero dei pixel di fondo cielo utilizzati nella stima del livello medio di fondo cielo;
G = guadagno (gain) del CCD (electroni/ADU)
σf2 = stima dell'errore 1-sigma introdotto dal convertitore A/D: il suo valore può essere approssimato a 0.289.
Vediamo un esempio pratico con qualche numero reale. Il CCD è un SITe502 con queste caratteristiche (dalla scheda tecnica del modello Apogee AP7p):
G = 4.4 elettroni / ADU
NR = 10.2 elettroni
ND = 1.4 elettroni / pixel / secondo (a temp. -27 Gradi.)
Supponiamo una esposizione di 60 secondi ad una temperatura di -27 gradi e, per semplicità, che la scala immagine CCD è di 3 arcsec / pixel e che il seeing sia tale da permettere al segnale proveniente dalla stella di ricadere completamente nel raggio di 1 pixel: dopo la sottrazione del valore del fondo cielo, nel nostro pixel troviamo Ns = 12015 ADU ∙ G = 12015 ∙ 4,4 = 52866 elettroni. Supponiamo anche di misurare il il fondo cielo all'interno di una box di 20x20 pixel vicino alla stella e che si trovi un valore medio di 3215 ADU / pixel (quindi NB = 3215 ∙ G = 14146 elettroni).
Sostituendo questi valori nella Eq. 2 si ottiene (si noti che tutti i valori utilizzati sono espressi in elettroni, non in ADU):
Con questi numeri si può facilmente notare che se si ignora il secondo termine al divisore, il SNR assume il valore ideale di un puro rumore di Poisson:
e che, se prendiamo in considerazione le condizioni del fondo cielo, la corrente di buio e il rumore di lettura solo abbiamo ancora:
Si noti che è possibile utilizzare la seguente formula semplificata senza fare un grande errore:
Oppure, se siamo interessati a una previsione del valore SNR che può essere ottenuto per un dato sistema CCD e un tempo di integrazione t, l' Eq. 3 può essere scritta come:
dove Ns, NB e ND, ora sono da intendersi come conteggi in elettroni (fotoni) al secondo se t è espresso in secondi. Questa equazione illustra una regola empirica preziosa relativa SNR di un'osservazione: il SNR è proporzionale a √ t e non di t stesso.








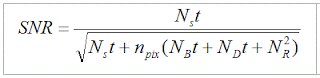
4 commenti:
Come prima cosa i ringraziamenti sono dovuti, sia per il blog che porti avanti, sia per il magnifico lavoro svolto con Astroart. Ma veniamo al post. Mi sembra tutto decisamente chiaro, però c'è qualcosa che in realtà non ho ben capito. Ad un certo punto porti come esempio un conteggio pari a 900 derivante da una certa sorgente (500 conteggi) e dal fondo (400 conteggi). Affermi non essere pari a 30 l'SNR per motivi chiari e poni come stima migliore 500/900 = √16,7 (Qui forse c'è un refuso dovrebbe essere: 500/√900 = 16,7 giusto?)
Ma veniamo alla domanda. Non mi è chiaro il motivo della formula successiva, nella quale il fattore al denominatore contiene due volte il contributo del fondo cielo.
Grazie. Paolo
Grazie Paolo! In effetti è un refuso che ho prontamente corretto, grazie ancora. Per quanto riguarda la formula successiva, il concetto è poco intuitivo: il segnale della stella è "contaminato" due volte dal fondo cielo perché occorre considerarlo una prima volta come "inglobato" nel segnale della stella e una seconda volta quando, in fotometria, si sottrae il valore del fondo cielo da quello della stella. Qualunque operazione matematica applichi nel calcolo del rumore (somma, sottrazione, divisione ecc.) il rumore si somma SEMPRE quadraticamente.
Perfetto come sempre chiarissimo! Grazie.
complimenti... da un ex ricercatore bravo.... chapeaux...!:::!:
Posta un commento